MSK

MSK (Minimum Shift Keying) - вид частотной модуляции с минимальным разносом частот. Это более продвинутая версия CPFSK модуляции, которая имеет непрерывную фазу, но у которой индекс модуляции, отвечающий за расстояние между частотами для нуля и единицы, минимален.

Модуляция MSK

Перед переходом к MSK рекомендую ознакомиться с CPFSK и FSK модуляциями. Ссылки на эти модуляции можно найти на главной странице моего сайта. Главным отличием MSK от CPFSK является ширина спектра. В MSK он минимален, что позволяет использовать все плюсы CPFSK и занимать еще меньше полосы пропускания. Разберемся немного лучше на что влияет индекс модуляции и где найти его в формулах. При обычной CPFSK модуляции мы выбираем базовую частоту и уже на ее основе определяем две другие частоты, одну для нуля, вторую для единицы.

\begin{matrix} w_{b a s e} = 50 \\ w_{d e v i a t i o n} = p i * (1 / T b) * f s k_{i n d e x} \end{matrix}

В приведенных формулах Tb - это длительность одного бита, а fsk_index и есть тот индекс, которым отличается CPFSK от MSK. Этот индекс напрямую влияет на разнос частот. Как видно из формул - чем больше индекс, тем больше разнос частот. Стандартные значения этого индекса: 1, 2, 3, 5. Посмотрим как меняется разнос частот в CPFSK при изменении этого индекса. Длительность одного бита будет равна 1 секунде.


xxxxxxxxxx
43
1
Fs = 1000;
2
Tb = 1;
3
t = 0:1/Fs:Tb-1/Fs;
4

5
fsk_indices = [0.1, 0.5, 1, 3, 5];
6
w_base = 50;
7
figure;
8

9
for idx = 1:length(fsk_indices)
10
    fsk_index = fsk_indices(idx);
11
    w_deviation = pi * (1/Tb) * fsk_index;
12

13
    w0 = w_base - w_deviation;
14
    w1 = w_base + w_deviation;
15

16
    bits = [0 1 0 0 1 0 0 0 0 1 1 0 0 1];
17

18
    phase = 0;
19
    CPFSK_signal = [];
20
    for i = 1:length(bits)
21
        if bits(i) == 0
22
            freq = w0;
23
        else
24
            freq = w1;
25
        end
26
        for j = 1:length(t)
27
            phase = phase + freq / Fs;
28
            CPFSK_signal = [CPFSK_signal cos(phase)];
29
        end
30
    end
31

32
    N = length(CPFSK_signal);
33
    f = (-N/2:N/2-1)*(Fs/N);
34
    Y_CPFSK = fftshift(fft(CPFSK_signal, N));
35
    P_CPFSK = abs(Y_CPFSK/N);
36

37
    subplot(length(fsk_indices), 1, idx);
38
    plot(f, P_CPFSK);
39
    title(['Spectrum of CPFSK Modulated Signal (fsk\_index = ', num2str(fsk_index), ')']);
40
    xlabel('Frequency (Hz)');
41
    ylabel('|P(f)|');
42
    xlim([-20 20]);
43
end

При запускаем получим 5 спектров сигналов с разными fsk_index: 0.1, 0.5, 1, 3, 5.

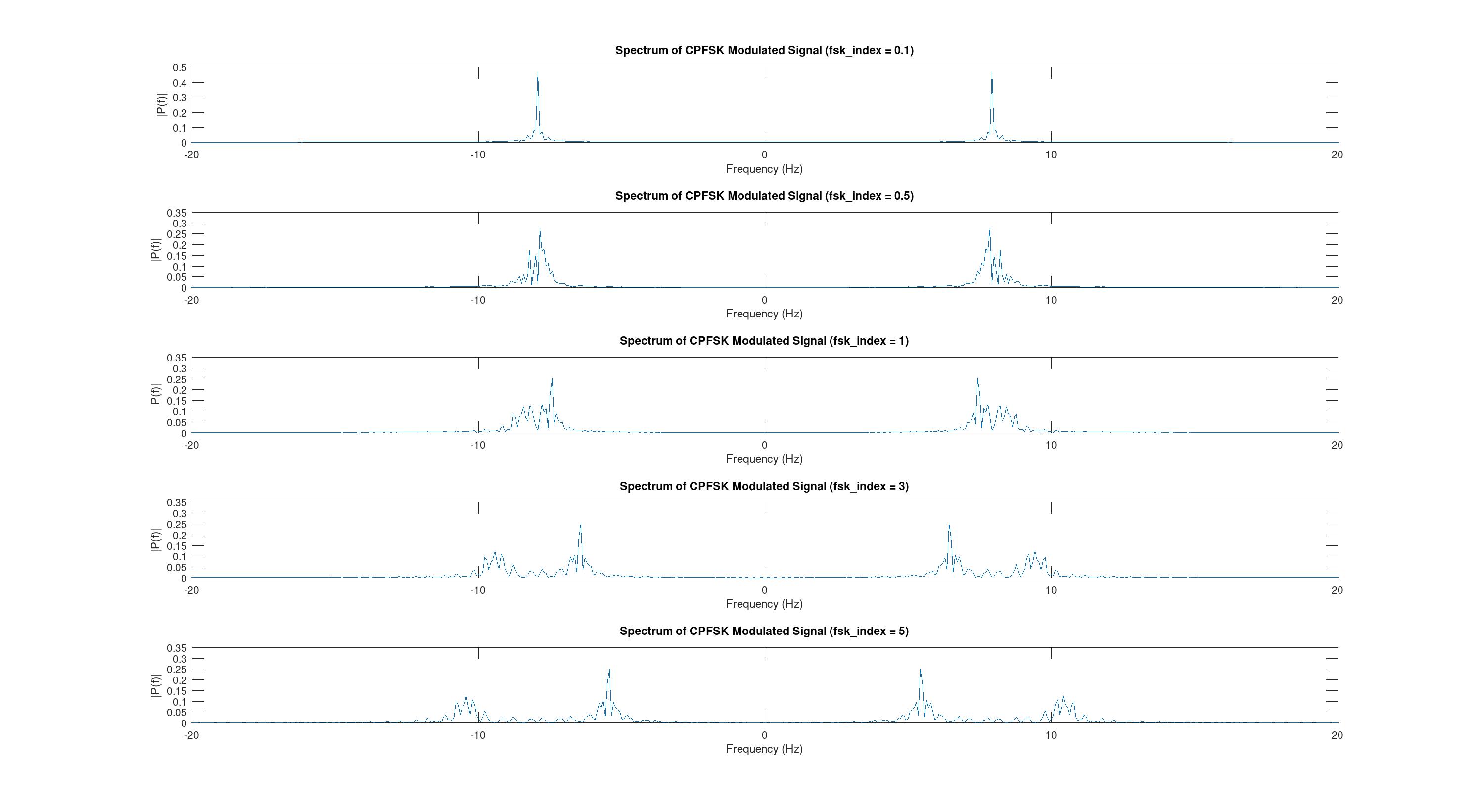
spectrs

На графике четко видно разницу между частотами при индексе 5, но при уменьшении индекса модуляции разница становится всё меньше. В какой-то момент, а именно при 0.5, различить на спектре частоты становится очень сложно, а при 0.1 вообще невозможно, потому что они сливаются в одну.

Минимальный индекс модуляции

Чтобы найти нужный индекс модуляции нужно решить задачу с ортогональностью несущих частот в сигнале. Ортогональность - это свойство двух функций или векторов, которые взаимно перпендикулярны в простанстве состояний, что в контексте сигналов означает, что их перекрестное влияние друг на друга минимально или вообще отсутствует. То есть задача ортогональности сводится к тому, чтобы найти такие частоты с минимальным разносом, которые бы не влияли друг на друга и смогли бы быть восстановлены при приеме и демодуляции сигнала.

Для двух функций f1(t) и f2(t), которые определены на интервале [a,b], они ортогональные если их скалярное произведение равно нулю. Математически это выглядит следующим образом.

\int_{a}^{b} f 1 (t) * f 2 (t) d t = 0

Если проецировать это на сигналы, то ортогональные несущие это сигналы, чьи частоты или фазы выбраны таким образом, чтобы они были ортогональны друг другу.

Рассмотрим пример с двумя сигналами с разными частотами.

\begin{matrix} s_{1} (t) = c o s (2 * p i * f_{1} * t) \\ s_{2} (t) = c o s (2 * p i * f_{2} * t) \end{matrix}

Эти сигналы будут ортогональными, если их скалярное произведение будет равно нулю. Подставим их в формулу с интегралом.

\int_{0}^{T} c o s (2 * p i * f_{1} * t) * c o s (2 * p i * f_{2} * t) d t = 0

Для гармонических функций с различными частотами это условие выполняется, если Т - период наименьшего общего кратного периодов двух сигналов. Интегрируя выражение получаем следующее. Заменим частоты на угловые и решим интеграл.

\begin{matrix} \int_{0}^{T} c o s (w_{1} * t) * c o s (w_{2} * t) d t = 0 \\ c o s (w_{1} * t) * c o s (w_{2} * t) = [c o s ((w_{1} - w_{2}) * t) + c o s ((w_{1} + w_{2}) * t)] / 2 \end{matrix}

Используя тригонометрическое тождество произведения косинусов и подставляем его в интеграл. Теперь можем разбить один большой интеграл на два.

\begin{matrix} \frac{1}{2} \int_{0}^{T} [c o s ((w_{1} - w_{2}) * t) + c o s ((w_{1} + w_{2}) * t)] d t \\ \frac{1}{2} (\int_{0}^{T} [c o s ((w_{1} - w_{2}) * t)] d t + \int_{0}^{T} [c o s ((w_{1} + w_{2}) * t)] d t) \end{matrix}

Теперь проанализируем два интеграла отдельно. Первый интеграл.

\int_{0}^{T} [c o s ((w_{1} - w_{2}) * t)] d t

Интеграл косинуса будет равен нулю, если его аргумент будет равен 2pi умноженному на любое целое число. Используя это свойство получаем.

(w_{1} - w_{2}) = \frac{2 * p i * k}{T}

Второй интеграл.

\int_{0}^{T} [c o s ((w_{1} + w_{2}) * t)] d t

Следуя прошлому правилу получаем.

(w_{1} + w_{2}) = \frac{2 * p i * m}{T}

В обоих случаях k и m - это константы отличные от нуля.

Вернемся к MSK. В MSK частоты f1 и f2 выбираются таким образом, чтобы сигналы были ортогональный. Частоты для 1 и 0 соответственно равны.

\begin{matrix} f_{0} = f_{b a s e} - Δ f \\ f_{1} = f_{b a s e} + Δ f \end{matrix}

Где f_base - центральная частота, а delta f - девиация частоты. Tb - длительность 1 бита. Тогда, для ортогональности частот f0 и f1.

\begin{matrix} (w_{1} - w_{2}) = 2 * p i * (f_{1} - f_{0}) = \frac{2 * p i * k}{T_{b}} \\ 2 * p i * ((f_{b a s e} + Δ f) - (f_{b a s e} - Δ f)) = \frac{2 * p i * k}{T_{b}} \\ 2 * p i * (2 * Δ f) = \frac{2 * p i * k}{T_{b}} \\ 4 * p i * Δ f = \frac{2 * p i * k}{T_{b}} \\ Δ f = \frac{k}{2 T_{b}} \end{matrix}

Так как k - это целое число не равное нулю, то его минимальное значение будет 1. Именно по этой формуле рассчитывается девиация частот для MSK, FSK и CPFSK. Она позволяет получить минимальную разницу между частотами и добиться наименьшей ширины спектра. Индекс модуляции для MSK можно получить используя формулу индекса модуляции через скорость передачи и девиацию частоты.

\begin{matrix} f s k_{i n d e x} = \frac{Δ f}{\frac{1}{T_{b}}} \\ f s k_{i n d e x} = \frac{\frac{1}{2 * T_{b}}}{\frac{1}{T_{b}}} \\ f s k_{i n d e x} = \frac{\frac{1}{2 * 1}}{\frac{1}{1}} \\ f s k_{i n d e x} = \frac{0.5}{1} = 0.5 \end{matrix}

Соответственно индекс модуляции для MSK всегда равен 0.5. Именно за счет ортогональности сигналов и низкого индекса модуляции мы получаем узкий спектр, что дает множество преимуществ MSK перед CPFSK.

Модуляция MSK в Octave

Изучим спектральную разницу между CPFSK с индексом модуляции 1 и MSK. Для этого используем следующим код.


xxxxxxxxxx
69
1
Fs = 1000;
2
Tb = 1;
3
t = 0:1/Fs:Tb-1/Fs;
4

5
w_base = 50;
6

7
fsk_index_cpfsk = 1;
8
w_deviation_cpfsk = pi * (1/Tb) * fsk_index_cpfsk;
9

10
w0_cpfsk = w_base - w_deviation_cpfsk;
11
w1_cpfsk = w_base + w_deviation_cpfsk;
12

13
bits = [0 1 0 0 1 0 0 0 0 1 1 0 0 1];
14

15
phase = 0;
16
CPFSK_signal = [];
17
for i = 1:length(bits)
18
    if bits(i) == 0
19
        freq = w0_cpfsk;
20
    else
21
        freq = w1_cpfsk;
22
    end
23
    for j = 1:length(t)
24
        phase = phase + freq / Fs;
25
        CPFSK_signal = [CPFSK_signal cos(phase)];
26
    end
27
end
28

29
N = length(CPFSK_signal);
30
f = (-N/2:N/2-1)*(Fs/N);
31
Y_CPFSK = fftshift(fft(CPFSK_signal, N));
32
P_CPFSK = abs(Y_CPFSK/N);
33

34
fsk_index_msk = 0.5;
35
w_deviation_msk = pi * (1/Tb) * fsk_index_msk;
36

37
w0_msk = w_base - w_deviation_msk;
38
w1_msk = w_base + w_deviation_msk;
39

40
phase = 0;
41
MSK_signal = [];
42
for i = 1:length(bits)
43
    if bits(i) == 0
44
        freq = w0_msk;
45
    else
46
        freq = w1_msk;
47
    end
48
    for j = 1:length(t)
49
        phase = phase + freq / Fs;
50
        MSK_signal = [MSK_signal cos(phase)];
51
    end
52
end
53

54
N = length(MSK_signal);
55
f = (-N/2:N/2-1)*(Fs/N);
56
Y_MSK = fftshift(fft(MSK_signal, N));
57
P_MSK = abs(Y_MSK/N);
58

59
figure;
60
plot(f, P_CPFSK, 'r', 'DisplayName', 'CPFSK (fsk\_index = 1)');
61
hold on;
62
plot(f, P_MSK, 'b', 'DisplayName', 'MSK (fsk\_index = 0.5)');
63
title('Spectr of CPFSK and MSK Modulated Signals');
64
xlabel('Frequency (Hz)');
65
ylabel('|P(f)|');
66
xlim([-20 20]);
67
legend('show');
68
hold off;
69

При запуске получаем следующие графики.

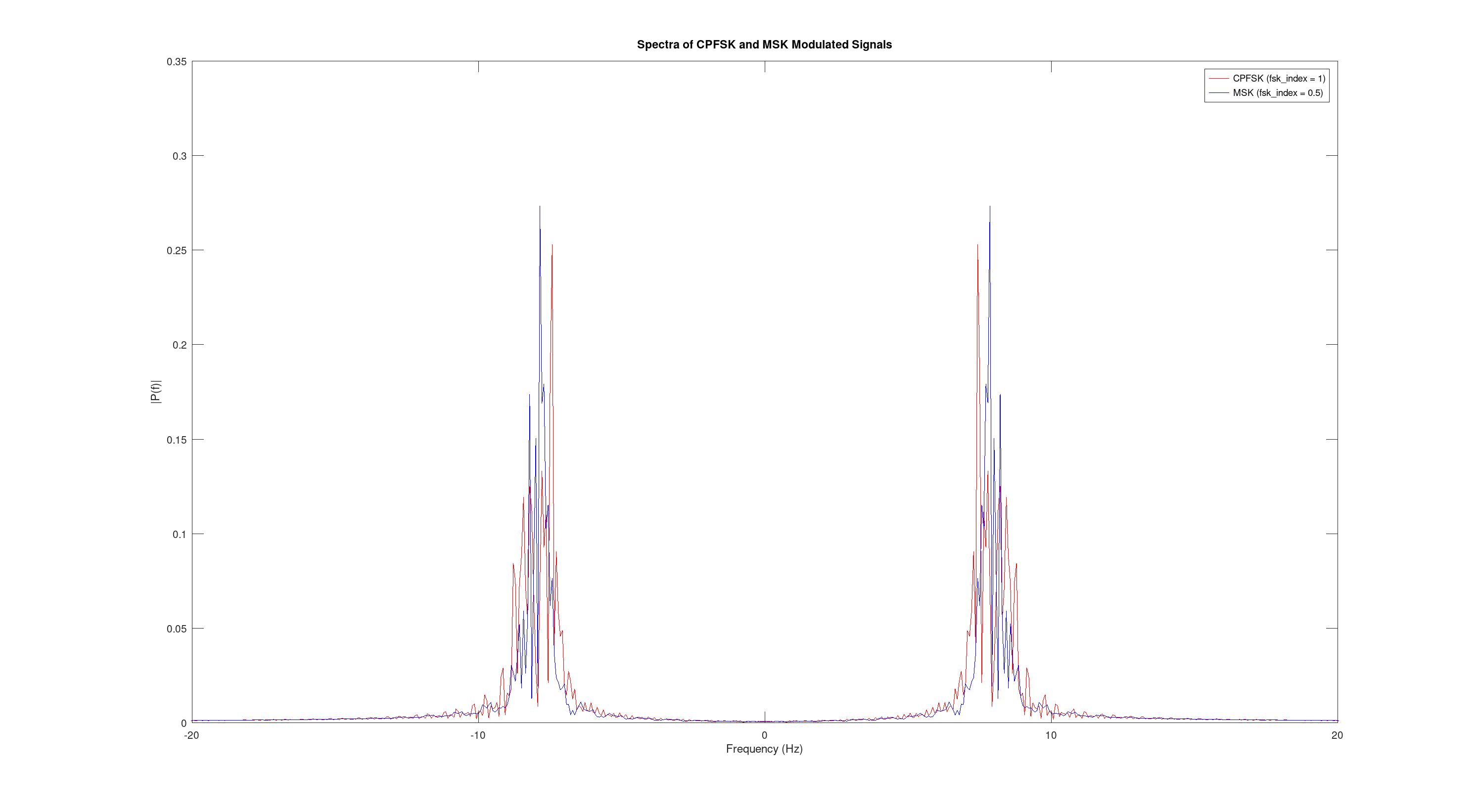
spectrs

Как видно спектр MSK немного уже спектра CPFSK. Это позволяет более эффективно использовать полосы частот, снизить межканальные помехи и улучшить устойчивость к шуму.

Ресурсы

https://ru.dsplib.org/content/signal_msk/signal_msk.html#:~:text=MSK%20%D0%BC%D0%BE%D0%B4%D1%83%D0%BB%D1%8F%D1%86%D0%B8%D1%8F%20%D1%8D%D1%82%D0%BE%20%D1%87%D0%B0%D1%81%D1%82%D0%BD%D1%8B%D0%B9%20%D1%81%D0%BB%D1%83%D1%87%D0%B0%D0%B9,%D0%B8%20%C2%AB1%C2%BB%20(%D1%82. https://digteh.ru/UGFSvSPS/modul/MSK/