FSK

Модуляция FSK одна из подвидов частотной модуляции. Она является одной из самых распространенных в цифровой связи за счет своей простоты в модуляции и демодуляции.

Модуляция FSK

В примерах рассмотрим цифровую версию FSK (BFSK) модуляции и проведем эксперименты с ней в Octave. Для начала необходимо определиться с модулирующим сигналом, он будет представлять собой двоичную последовательность нулей и единиц с определенной битовой скорость BPS (bits per second). Исходный сигнал будет иметь следующий вид.

0 1 0 0 1 0 0 0 0 1 1 0 0 1

В самом простом виде для модуляции сигнала в FSK используется два генератора с разными частотами. В зависимости от модулирующего сигнала мы используем либо первый генератор g0, либо второй генератор g1. Схема устройства для модуляции выглядит следующим образом.

[g0] ->        
        \__ switch ---> signal 
[g1] ->        ^-- source digital signal

Переключатель switch меняет положение ключа в зависимости от сигнала, который приходит из исходного сигнала. Если передать 1 на вход ключа, то мы получим сигнал g0 на выходе, а если передать 0, то на выходе будет g1. Такая схема на практике применяется редко, так как найти переключатель, который сможет успевать переключаться с нужной скоростью довольно трудно. Вместо этого используются цифровые схемы и логика.

Модуляция FSK в Octave

Рассмотрим модуляцию с математической точки зрения в Octave. Для этого объявим несущую частоту, частоту девиации, длительность сигнала и два массива, один из которых - наши исходные данные, а второй - готовый сигнал.

Fs = 1000;             
Tb = 1;                
t = 0:1/Fs:Tb-1/Fs;    

% Частота девиации
fsk_index = 5
w_deviation = pi * (1/Tb) * fsk_index
w_base = 10

f0 = w_base - w_deviation;                
f1 = w_base + w_deviation;               

bits = [0 1 0 0 1 0 0 0 0 1 1 0 0 1];


FSK_signal = [];

Частота семплирования в 1000 Герц, длительность одного бита равна 1 секунде. Вектор времени рассчитывается на основе Fs и Tb. Формула частоты девиации рассчитывается на основе Tb и fsk_index таким образом, чтобы спектры в конечном сигнале были явно различимы. FSK_INDEX подбирается индивидуально под задачи. Частоты w0 и w1 рассчитываются на основе базовой частоты и частоты девиации.

for i = 1:length(bits)
    if bits(i) == 0
        FSK_signal = [FSK_signal cos(f0*t)];
    else
        FSK_signal = [FSK_signal cos(f1*t)];
    end
end

Для каждого бита в массиве bits создан программный переключатель в виде if. При 0 используем w0, а при 1 w1. Чтобы исследовать результаты в визуальном формате можно добавить следующим код.

figure;

subplot(3,1,1);
plot(t, cos(w0*t));
title('Frequency for bit 0');
xlabel('Time (s)');
ylabel('Amplitude');

subplot(3,1,2);
plot(t, cos(w1*t));
title('Frequency for bit 1');
xlabel('Time (s)');
ylabel('Amplitude');

subplot(3,1,3);
plot(0:1/Fs:(length(FSK_signal)-1)/Fs, FSK_signal);
title('FSK Modulated Signal');
xlabel('Time (s)');
ylabel('Amplitude');

В итоге конечный скрипт выглядит следующим образом.

Fs = 1000;
Tb = 1;
t = 0:1/Fs:Tb-1/Fs;

% Частота девиации
fsk_index = 5
w_deviation = pi * (1/Tb) * fsk_index
w_base = 50

w0 = w_base - w_deviation;
w1 = w_base + w_deviation;

bits = [0 1 0 0 1 0 0 0 0 1 1 0 0 1];


FSK_signal = [];

for i = 1:length(bits)
    if bits(i) == 0
        FSK_signal = [FSK_signal cos(w0*t)];
    else
        FSK_signal = [FSK_signal cos(w1*t)];
    end
end

figure;

subplot(3,1,1);
plot(t, cos(w0*t));
title('Frequency for bit 0');
xlabel('Time (s)');
ylabel('Amplitude');

subplot(3,1,2);
plot(t, cos(w1*t));
title('Frequency for bit 1');
xlabel('Time (s)');
ylabel('Amplitude');

subplot(3,1,3);
plot(0:1/Fs:(length(FSK_signal)-1)/Fs, FSK_signal);
title('FSK Modulated Signal');
xlabel('Time (s)');
ylabel('Amplitude');

При запуске наблюдаем следующие графики.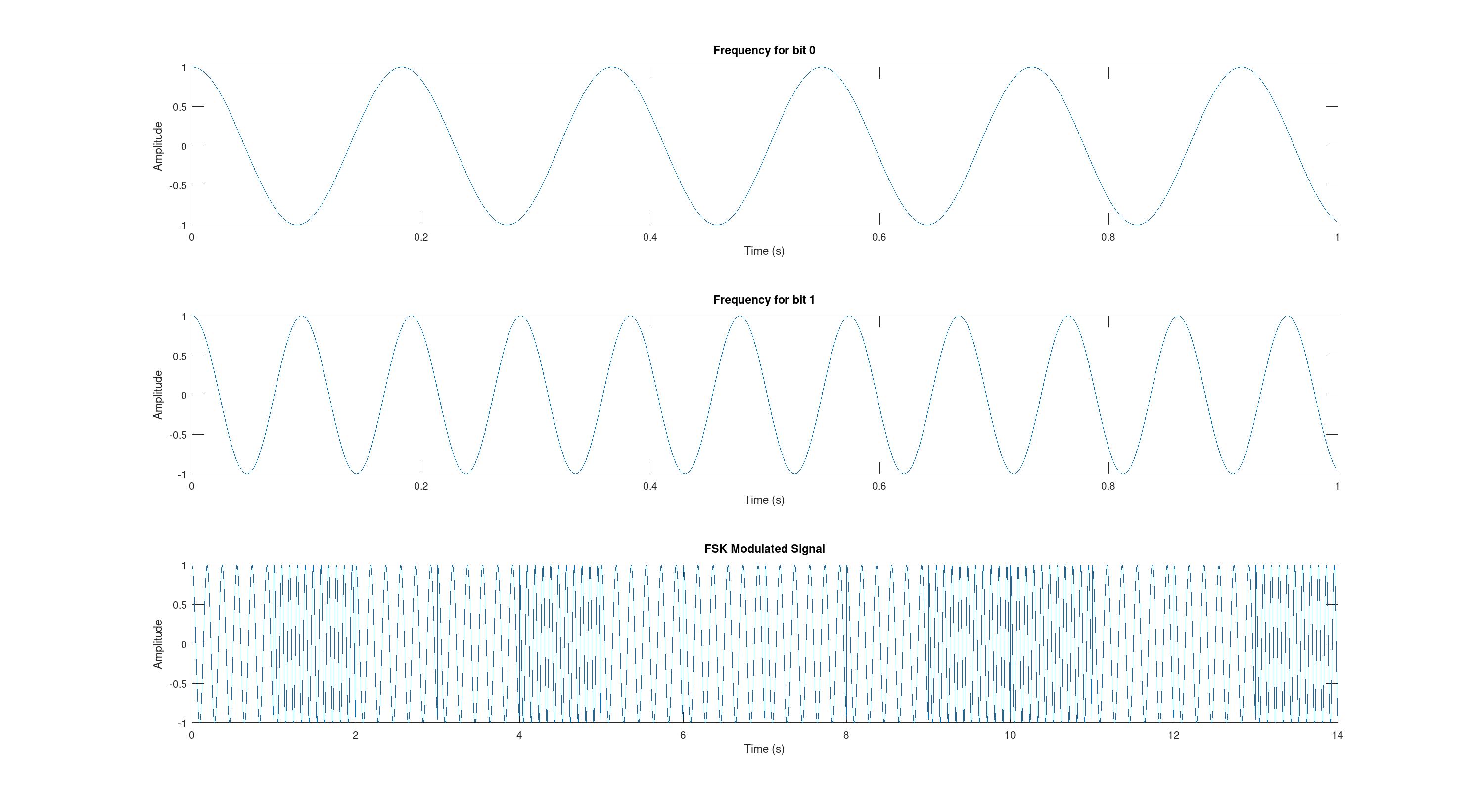

Спектр FSK сигнала

Перед изучением спектра в Octave остановимся на теоретической части. По сути спектр FSK сигнала есть сумма спектров двух исходных сигналов, то есть S = S(f0) + S(f1). В идеальных усливиях на спектре будет только две основные компоненты с частотами соответствующими логическим 0 и 1, в реальности же будет множество дополнительных гармоник. Легко проверить это на деле использовав быстрое преобразование Фурье.

xxxxxxxxxx
N = length(FSK_signal); 
f = (-N/2:N/2-1)*(Fs/N);

Y_f0 = fftshift(fft(cos(w0*t), N));
Y_f1 = fftshift(fft(cos(w1*t), N));
Y_FSK = fftshift(fft(FSK_signal));

P_f0 = abs(Y_f0/N);
P_f1 = abs(Y_f1/N);
P_FSK = abs(Y_FSK/N);

После этого можно изучить спектр исходных сигналов и готового FSK модулированного сигнала.

figure;

subplot(3,1,1);
plot(f, P_f0);
title('Centered Spectrum of Frequency for bit 0');
xlabel('Frequency (Hz)');
ylabel('|P(f)|');
xlim([-50 50]);

subplot(3,1,2);
plot(f, P_f1);
title('Centered Spectrum of Frequency for bit 1');
xlabel('Frequency (Hz)');
ylabel('|P(f)|');
xlim([-50 50]);

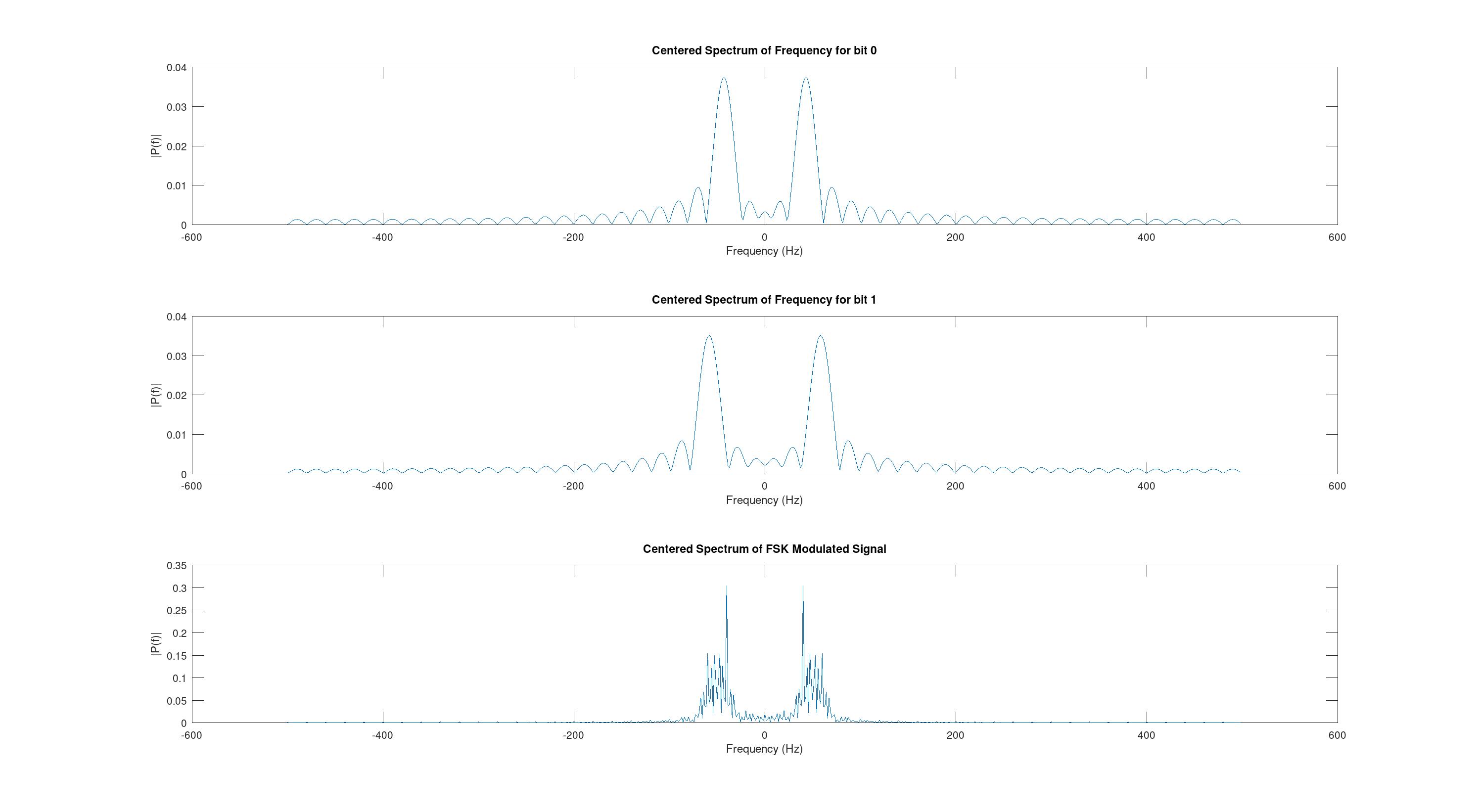
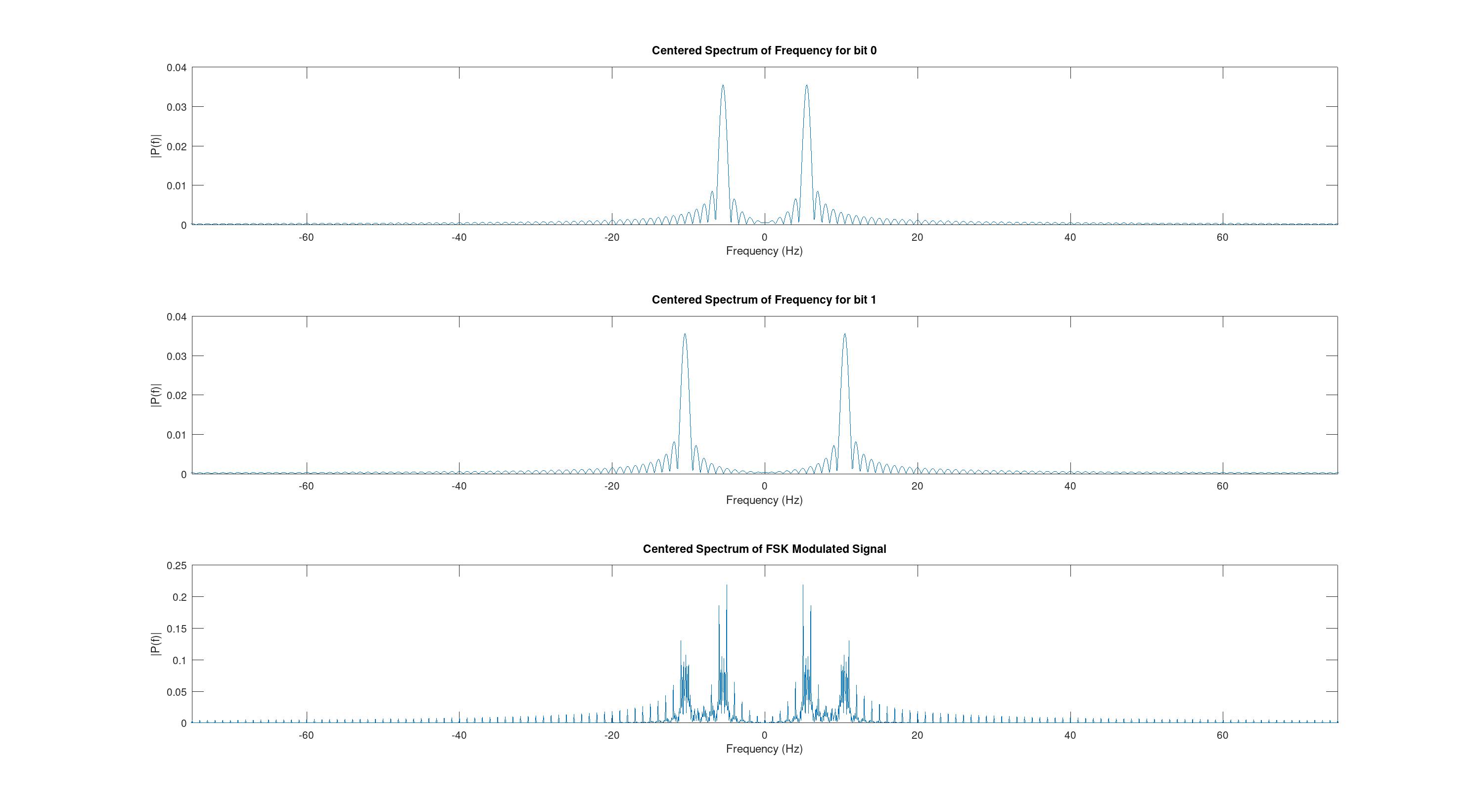
subplot(3,1,3);
plot(f, P_FSK);
title('Centered Spectrum of FSK Modulated Signal');
xlabel('Frequency (Hz)');
ylabel('|P(f)|');
xlim([-50 50]);

Получаем следующие графики.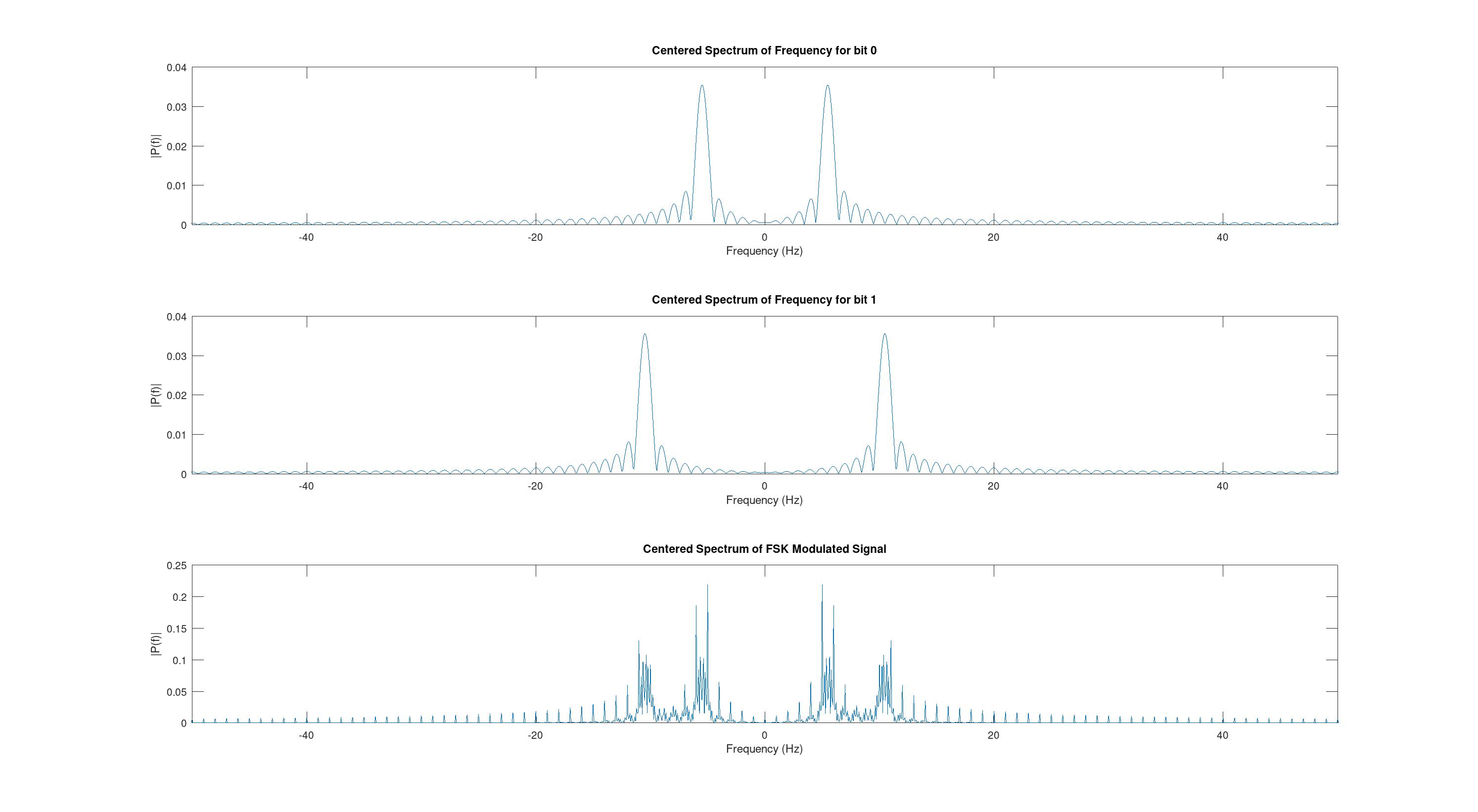

Как видно спектры исходных сигналов просто сложились. Видно, что составляющие сигнала разнесены друг от друга на какой-то определенный промежуток, который зависит от битовой скорость и индекса FSK (FSK_INDEX). Рассмотрим различную скорость передачи сигналов и изучим их спектральные графики. Для эксперимента рассмотрим скорость 0.5, 0.1 и 0.05.

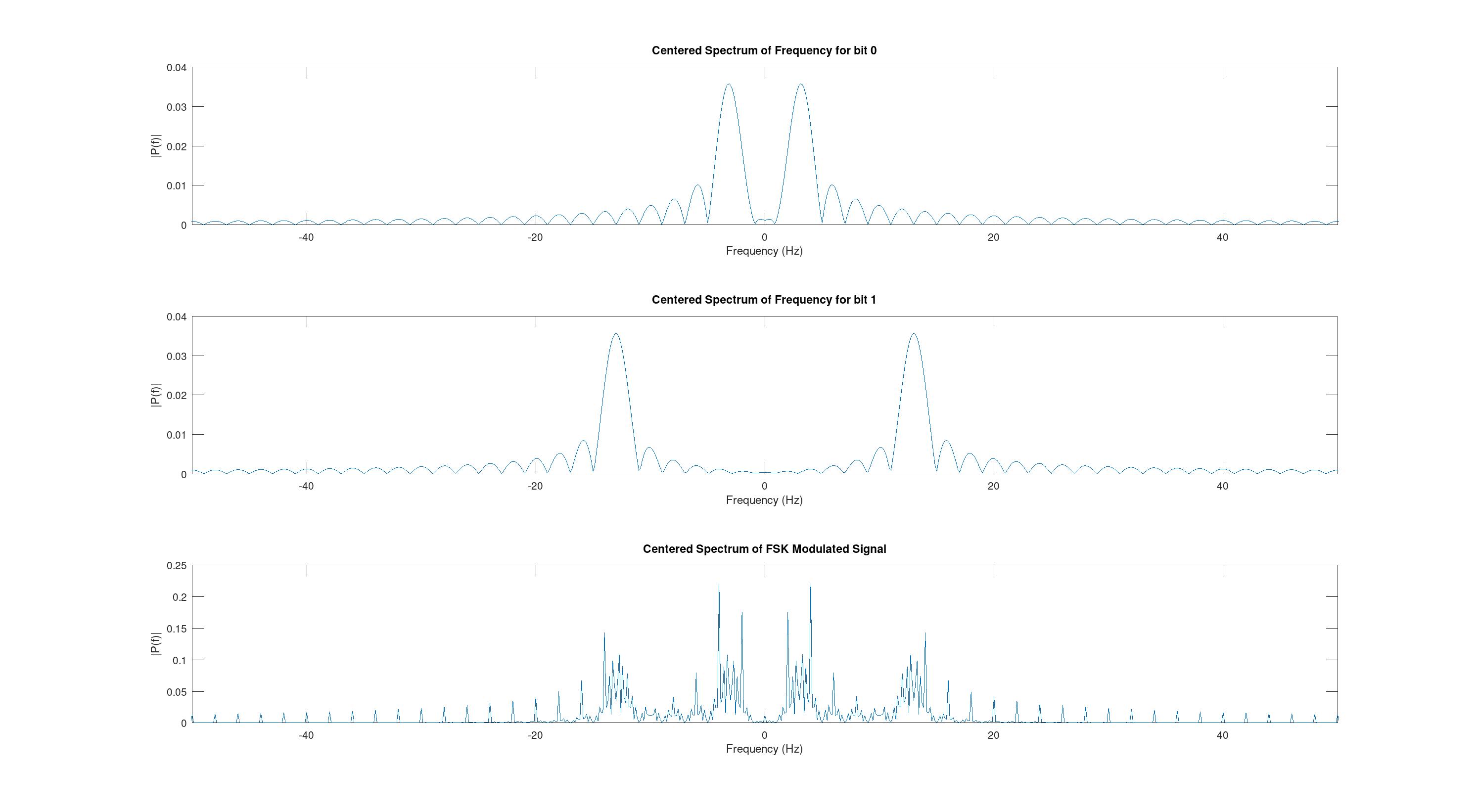
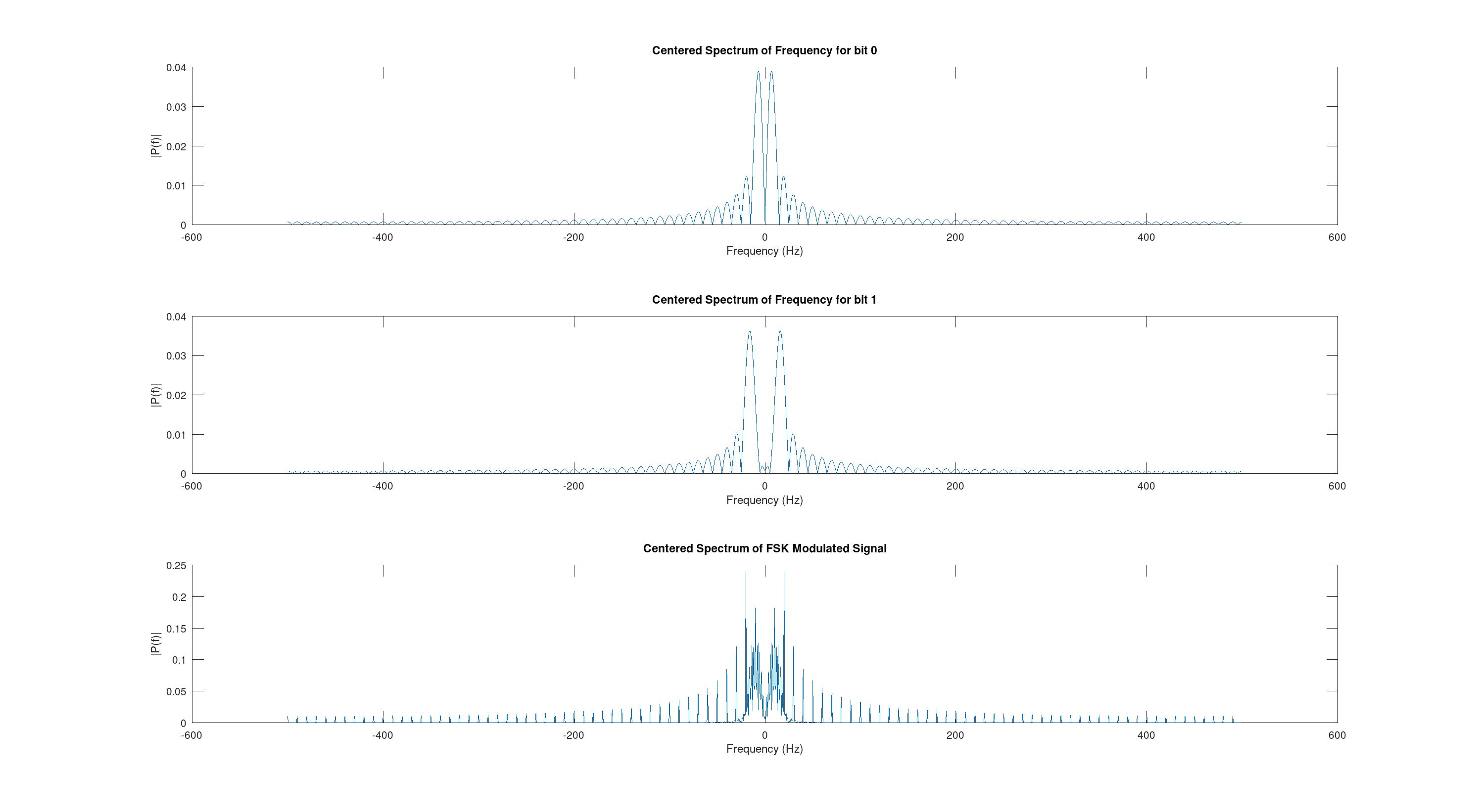
Общий график для сравнения 0.5, 0.1 и 0.05.

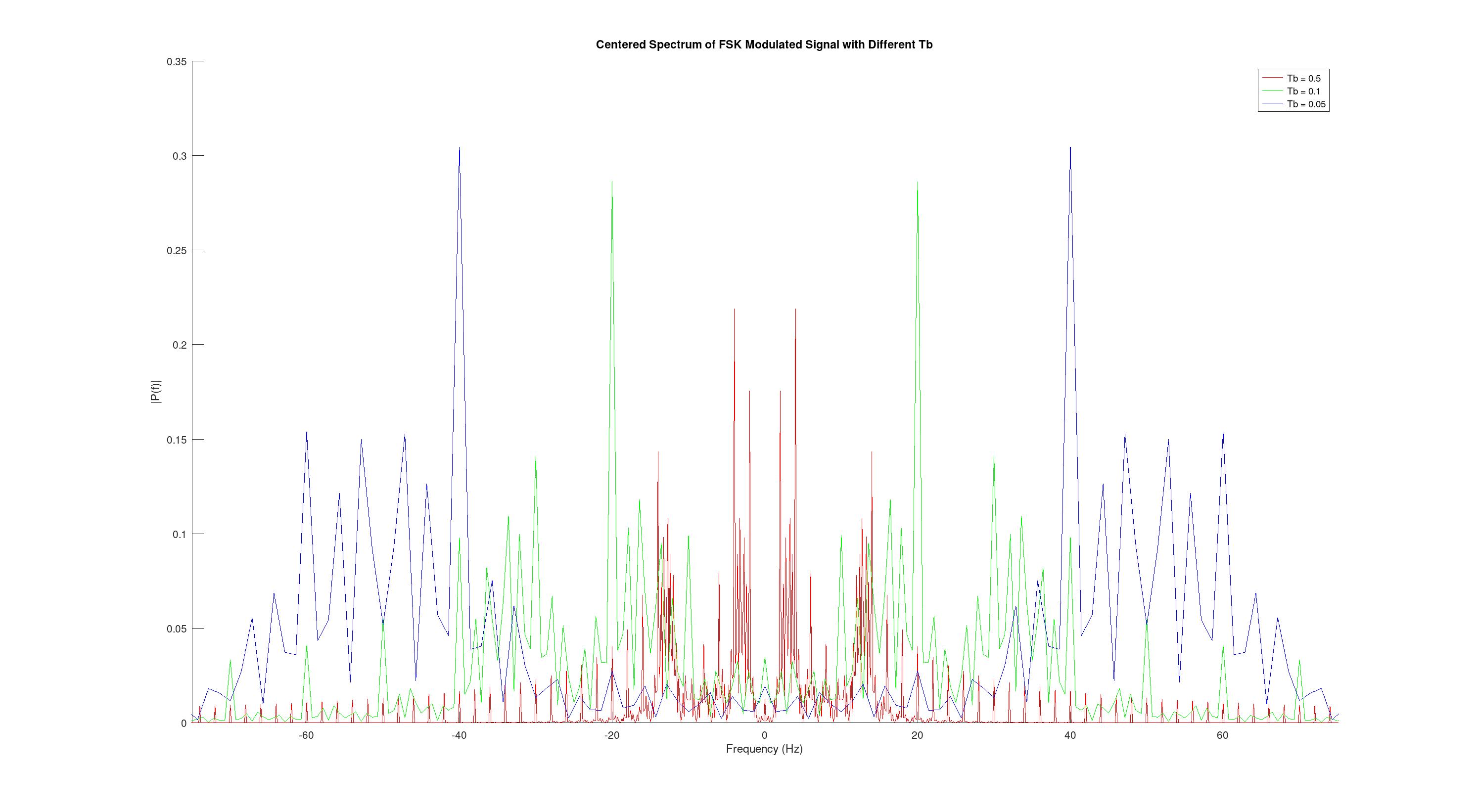
Из этого можно сделать вывод, что разнесение частот зависит напрямую от BPS, то есть от битовой скорость. Исходя из этого можно отметить, что ширина спектра зависит от скорости передачи данных и при больших скоростях спектр может быть довольно широким, в связи с этим при больших скоростях используются другие модуляции.

Связь битовой скорости и девиации частот можно проследить по следующим формулам. Начнем с частоты девиации.

xxxxxxxxxx
deviation = f1 - f0

Теперь можно связать частоту девиации со скоростью данных, это делается в Формуле Карсона.

https://www.rose-hulman.edu/DSPFirst/visible3/chapters/03spect/demosLV/spectrog/carson/carsonf.htm https://en.wikipedia.org/wiki/Carson_bandwidth_rule

xxxxxxxxxx
B = deviation + BPS/2

Где B - ширина спектра, dF - частота девиации, а BPS - битовая скорость. При увеличении битовой скорости заметно увеличивается ширина спектра, так как сигналы быстрее переключаются между частотами. Становятся более заметными боковые полосы, так как увеличение скорости приводит к большому спектральному разбросу. При уменьшении скорости происходит обратное выше описанному. Всё это мешает увеличивать скорость передачи данных и при большой скорости FSK становится бесполезным, так как спектры накладываются друг на друга и становится невозможно отличить их.

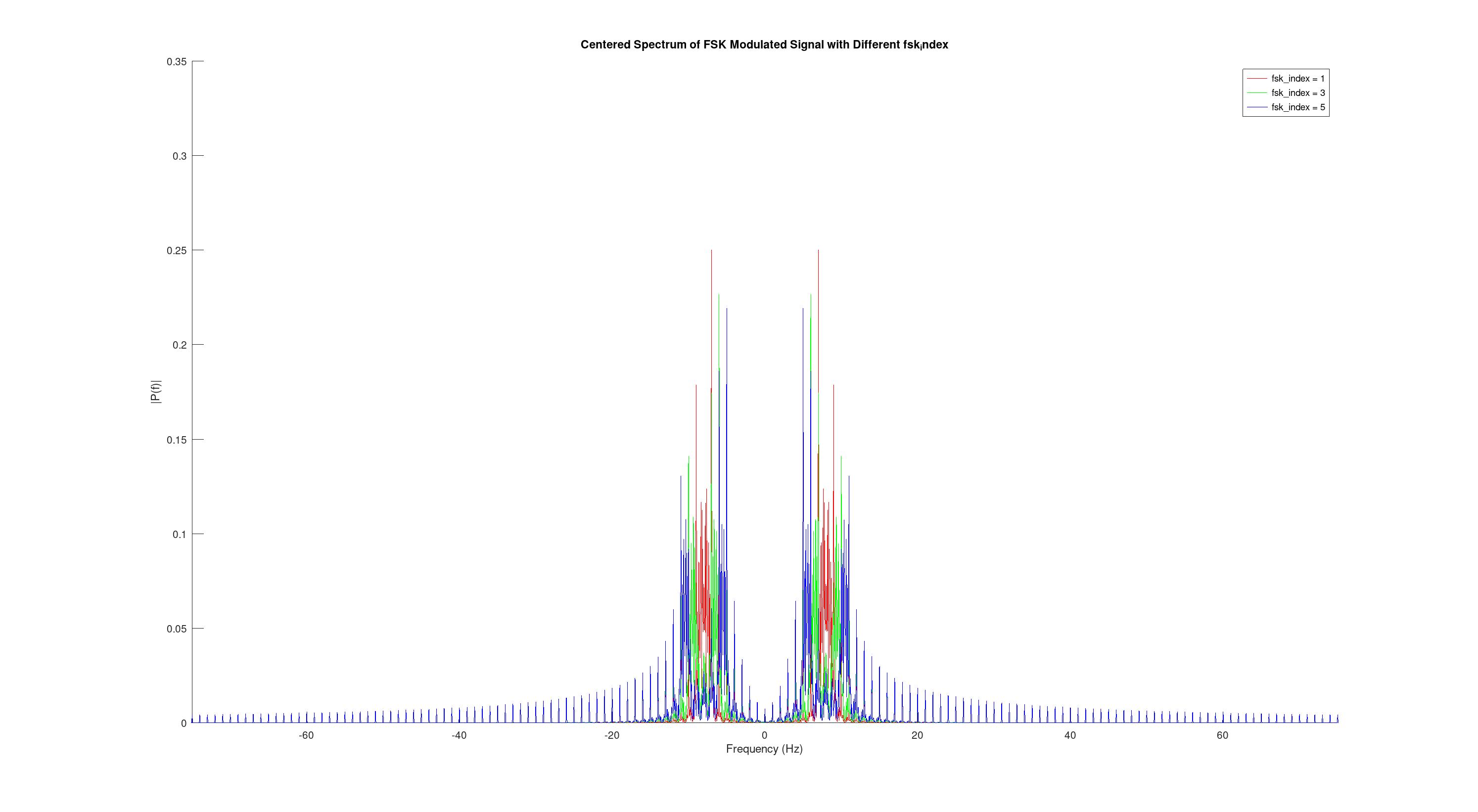
Рассмотрим также изменение спектра при изменении FSK_INDEX. Проверим при 1,3,5.

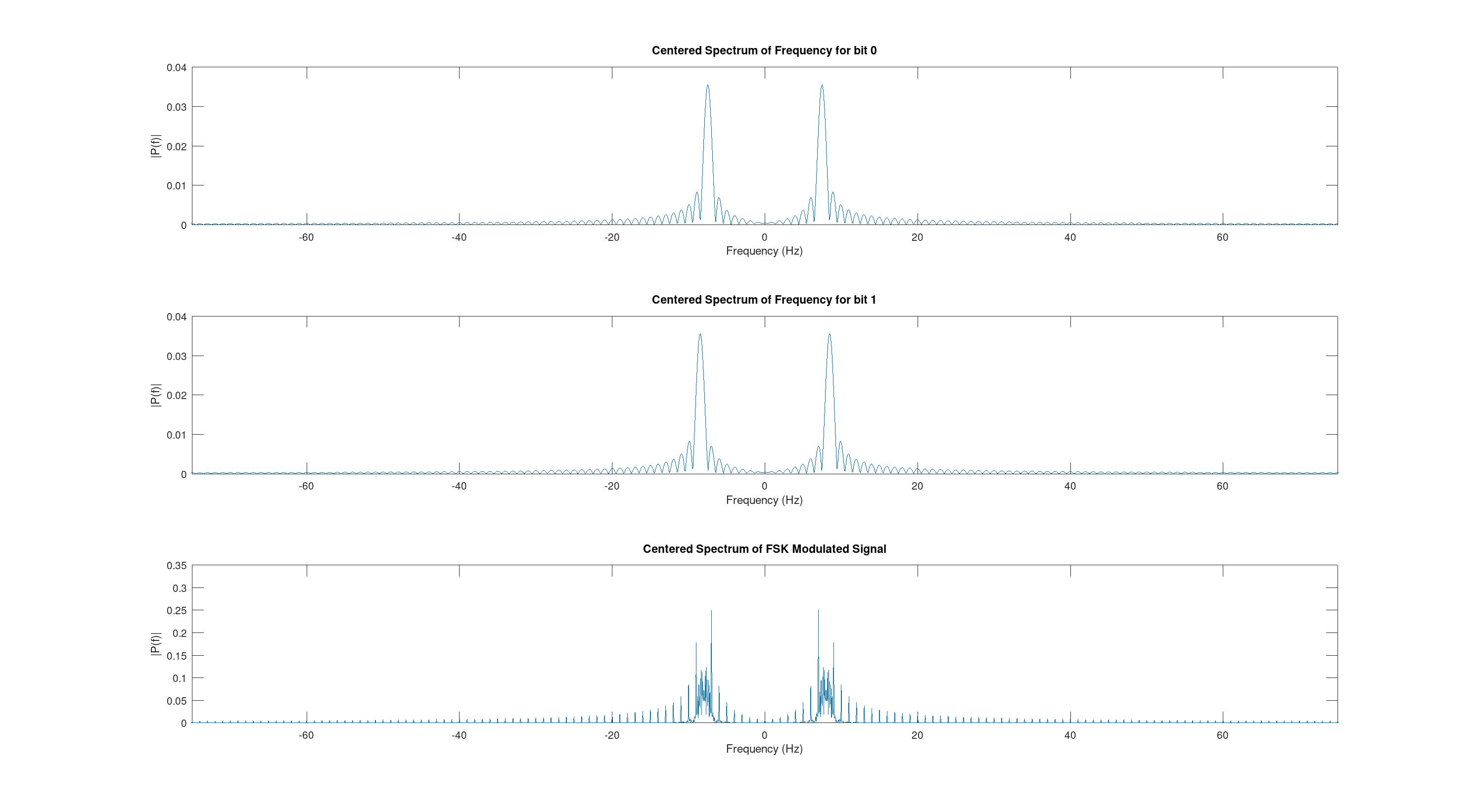
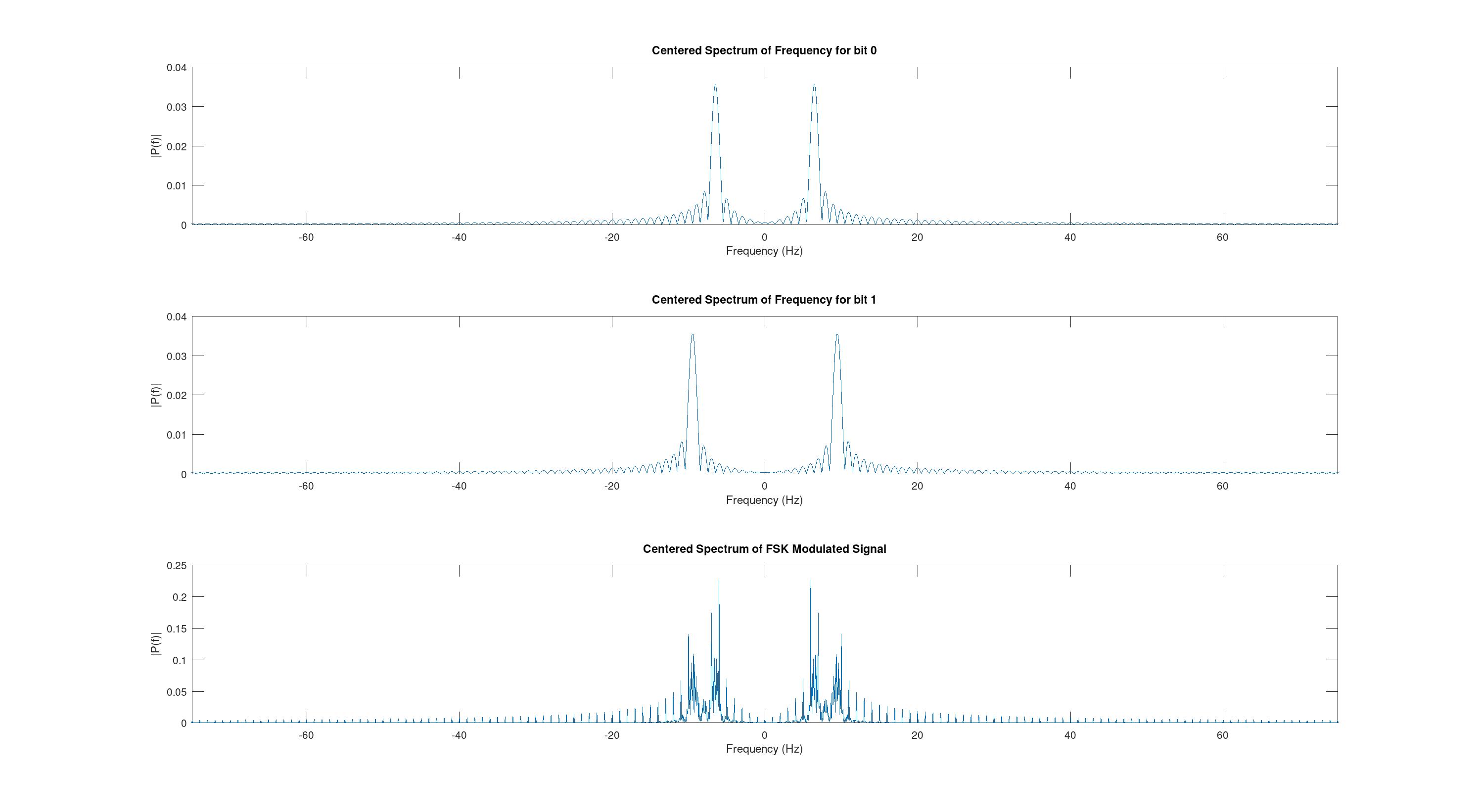
Также общий график для сравнения.

Ресурсы

https://www.rose-hulman.edu/DSPFirst/visible3/chapters/03spect/demosLV/spectrog/carson/carsonf.htm https://en.wikipedia.org/wiki/Carson_bandwidth_rule https://www.ntia.gov/sites/default/files/2023-11/j_2021_edition_rev_2023.pdf https://ru.dsplib.org/content/signal_fsk/signal_fsk.html#biblio https://github.com/daniestevez/gr-satellites/blob/b00658bc39cf29ef2518cd3274bee841ba1fd1e3/python/components/demodulators/fsk_demodulator.py#L77 https://www.radioscanner.ru/info/article345/